fpfc [openECSC 2024 (2nd Round)]
Challenge Description
Behold the newest technology! Our floating point flag checker will surely block all hackers from discovering our flags!
< this is a remote challenge >
Intuition
This was such a fun challenge and rather difficult in my opinion. Coming from anti-rev, I tried to angr1 my way through this challenge as well. At the time, I didn’t have too much experience with it, so it took me a while to realize that this approach was not really feasible. First of all, because of the difficult setup for providing input, and second of all, because I figures some more details while statically analysing the binary which made me scrap the angr attempt entirely.
What lead me to the solution was a patient and careful static analysis of the given program. There are multiple important observations that I managed to make:
First Input check
At first a basic input check is performed. The input will be deemed invalid if:
- it’s length is 0;
- if the length is not a multiple of 4;
- if there is at least one bytes of the input which does not correspond to an upper-case letter from the English alphabet;
puts("Checking your input...");
in_size = strlen(secret);
if ((in_size == 0) || ((in_size & 3) != 0)) {
puts("Invalid input");
ret_val = -1;
}
else {
for (i = 0; (ulong)(long)i < in_size; i = i + 1) {
if ((secret[i] < 'A') || ('Z' < secret[i])) {
puts("Invalid input");
ret_val = -1;
goto FAIL;
}
}
...
Decoding the input
The input data is then decoded 4 bytes, or rather letters, at a time. What we get is an angle expressed in radians between $0$ and $2 * \pi$ and a positive magnitude with values between $0$ and $25$. Each value is obtained by combining and converting a number in base 26 written with two English letters, into a number in base 10 with the maximum value of 675, mapping that value to the interval $[0, 1]$ and then scaling it back up by $\pi$ and $25$ respectively. The values are then stored into a vector, the type of which I set to a custom structure.
void init_g(char *secret,size_t size_div_4)
{
char cVar1;
char cVar2;
float fVar3;
int i;
for (i = 0; (ulong)(long)i < size_div_4; i = i + 1) {
cVar1 = secret[(long)(i << 2) + 2];
cVar2 = secret[(long)(i << 2) + 3];
fVar3 = (float)((int)secret[(long)(i << 2) + 1] + (secret[i << 2] + -0x41) * 0x1a + -0x41) /
675.0;
g_in_buff[i].angle = (fVar3 + fVar3) * 3.141593;
g_in_buff[i].mag_25 = ((float)((int)cVar2 + (cVar1 + -0x41) * 0x1a + -0x41) / 675.0) * 25.0;
}
return;
}
Each angle / magnitude pair can be interpreted as a vector in the XY plane. To me, this wasn’t obvious at all in the beginning. At first, I was only thinking about triangles 📐.
Processing the input
This is where it gets really interesting and more complex geometrically. For each angle / magnitude pair in the input a process_pair function is called. As part of the process_pair function some calculations are performed in a loop, which include calling another function geom_ops. The operations are performed while a variable R, initially equal to the current vector magnitude is greater than 0. We notice a number of interesting details:
process_pair: there is a global (x, y) coordinate pair (g_point) initialised with (100, 90). I deduced this is the starting point. Starting point of what? We’ll see later on;process_pair: the current vector is applied to theg_pointto obtain a transition segment. Thegeom_opsfunction is initially called on this segment (as a relative point fromg_point), the magnitude of the vector and the angle of the vector;p.x = g_point.x; p.y = g_point.y; mag = pair.mag_25; R = mag; angle = pair.angle; alpha = angle; while (g_point.x = p.x, g_point.y = p.y, 0.0 < R) { _T = (double)R; cos_alpha = cos((double)alpha); x = (float)(cos_alpha * _T); __T = (double)R; sin_alpha = sin((double)alpha); y = (float)(sin_alpha * __T); p.x = p.x + x; p.y = p.y + y; geom_ops(&p,&R,&alpha); }geom_ops: there is a global segments array (g_lines). This array is iterated and for each segment the program checks if that segment intersects the transition segment sent as a parameter. Some other checks and computations are performed if the segments intersect. I don’t fully understand the math from that part, but I have a pretty good intuition of what it does. If the segments don’t intersect nothing happens;for (i = 0; i < 195; i = i + 1) { line.X = g_lines[i].X; line.Y = g_lines[i].Y; intersect_res = intersect(&g_point,point,&line); if (intersect_res != 0) { /* if the segments intersect */ get_intersection(&I,&g_point,point,&line); point_dist = sqrtf((I.x - g_point.x) * (I.x - g_point.x) + (I.y - g_point.y) * (I.y - g_point.y)); if ((0.01 < point_dist) && (point_dist < length)) { p.x = I.x; p.y = I.y; beta = atanf((line.Y.y - line.X.y) / (line.Y.x - line.X.x)); ...main: after processing there is a final step in which theg_pointis checked to correspond to the origin coordinates pair (0, 0);
Taking everything into account, I could correctly deduce the high-level logic of the checker. The global segments array holds wall coordinates which form a labyrinth. We’re given a point g_point at a starting position of (100, 90). Our goal is to provide a set of moves which get the point to the origin. A move consists of pushing the point in any direction for at most 25 units of distance. If a point ends up touching a wall during a move the complex-ish math part that I mentioned becomes relevant. My educated guess is that the point will just bounce off each wall it encounters. This is somewhat difficult to simulate. HOWEVER, we can just avoid intersecting any walls with our moves and that way we avoid dealing with all that math. The task left is to find a path through the maze to the origin.
Other observations
It was crucial for me during the reverse engineering process that I could recognize some geometry algorithms, such as the one which determines if two segments intersect, or the one for finding the intersection point of two segments, thanks to some time spent on competitive programming during high-school. Chat-GPT could be helpful, but having the intuition won me time.
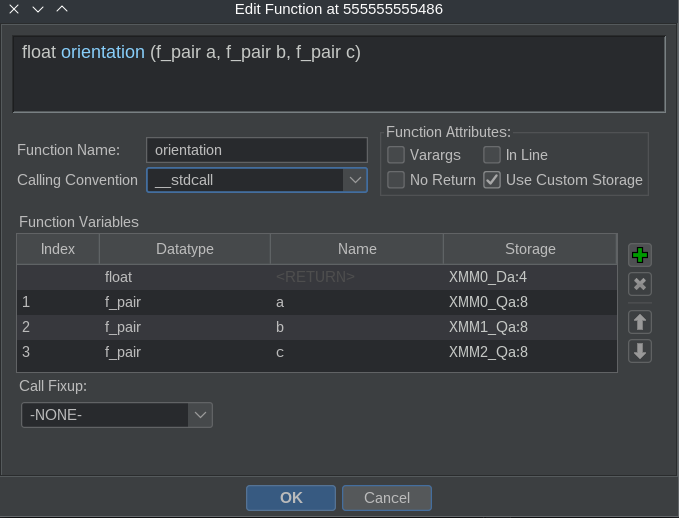
Due to floating point calculations, a lot of operations are done through with SSE instructions. That is why some functions passed parameters through the XMM registers. For some reason Ghidra did could not identify this calling convention and failed to decompile these functions. As a solution, I had to manually set the calling convention for the respective functions. With the change Ghidra could successfully decompile the machine code.
Solution
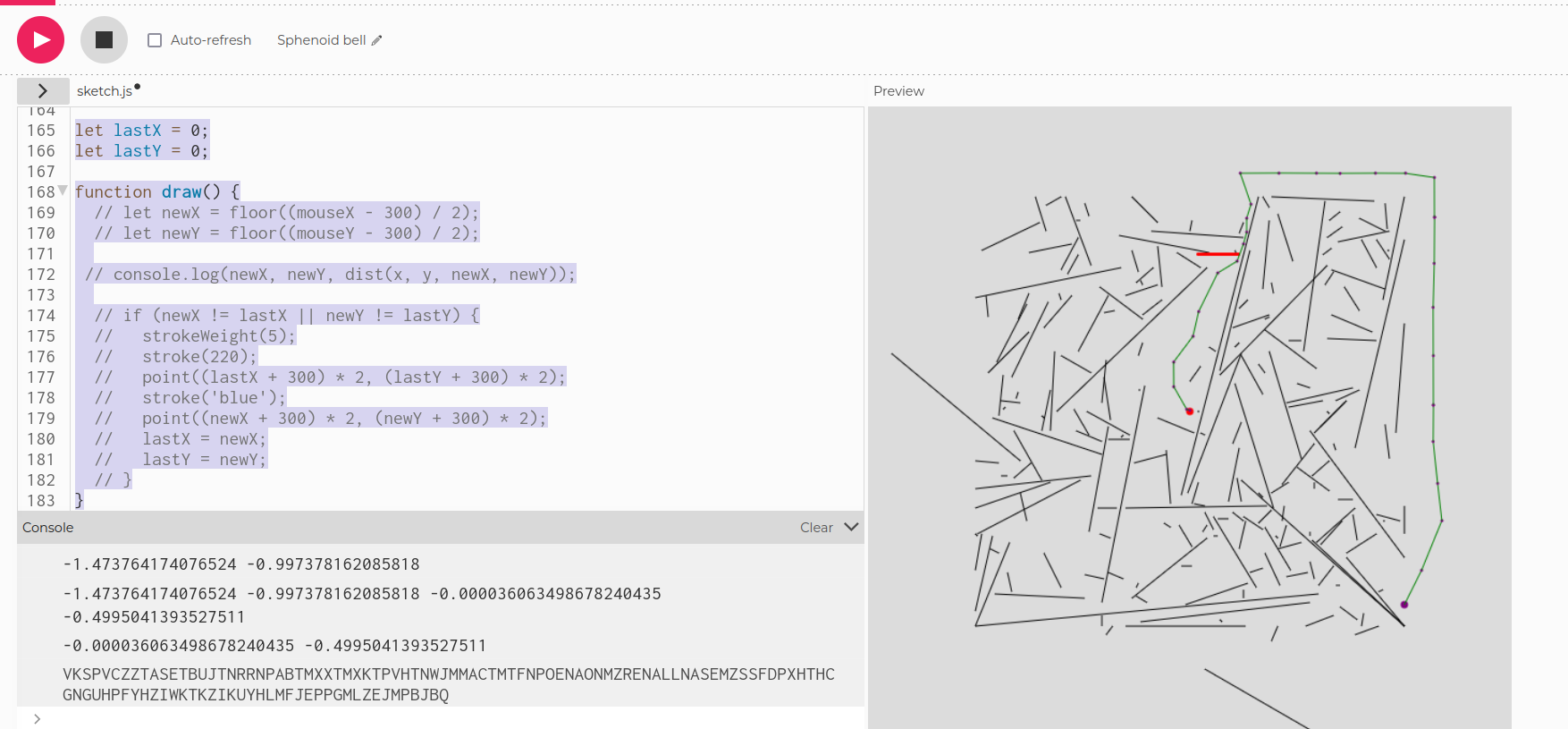
I build a p5.js 2 sketch with the extracted segments and starting point. On top of it I implemented a way to click on the map to add a new segment, which was checked using the same algorithm from the binary to not intersect any of the other segments. For precision reasons, I encoded and then decoded each point, and used the decoded values for calculations, as these differed slightly from the pre-encoding values. The payload is obtained by encoding each segment inputed on the map and stringing all these encodings together. You’ll find the full code of the sketch in the Appendix below.
Flag
openECSC{4lm0s7_l1k3_p1ng_pwng_0n_th3_w4llz_771ce3bd}
Appendix
let li = [ 0x00, 0x00, 0xc0, 0x41, 0x00, 0x00, 0x00, 0x42, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x00, 0xc2, 0x00, 0x00, 0x86, 0xc2, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0x54, 0xc2, 0x00, 0x00, 0x80, 0x42, 0x00, 0x00, 0x88, 0xc2, 0x00, 0x00, 0x60, 0x41, 0x00, 0x00, 0x88, 0xc1, 0x00, 0x00, 0xc2, 0xc2, 0x00, 0x00, 0x64, 0x42, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0x94, 0x42, 0x00, 0x00, 0xb8, 0xc2, 0x00, 0x00, 0x40, 0x40, 0x00, 0x00, 0x24, 0xc2, 0x00, 0x00, 0xa0, 0x41, 0x00, 0x00, 0x58, 0xc2, 0x00, 0x00, 0x80, 0xbf, 0x00, 0x00, 0x3c, 0xc2, 0x00, 0x00, 0x30, 0x41, 0x00, 0x00, 0x80, 0xc0, 0x00, 0x00, 0x1c, 0x42, 0x00, 0x00, 0x00, 0x42, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0x70, 0x42, 0x00, 0x00, 0xaa, 0x42, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0xb6, 0x42, 0x00, 0x00, 0x64, 0xc2, 0x00, 0x00, 0x84, 0x42, 0x00, 0x00, 0x84, 0xc2, 0x00, 0x00, 0x78, 0xc2, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x41, 0x00, 0x00, 0x86, 0xc2, 0x00, 0x00, 0xa8, 0xc1, 0x00, 0x00, 0x40, 0xc1, 0x00, 0x00, 0x24, 0xc2, 0x00, 0x00, 0xb2, 0x42, 0x00, 0x00, 0x60, 0x42, 0x00, 0x00, 0x60, 0x42, 0x00, 0x00, 0x60, 0x42, 0x00, 0x00, 0x68, 0x42, 0x00, 0x00, 0xb4, 0xc2, 0x00, 0x00, 0xb8, 0xc1, 0x00, 0x00, 0x98, 0xc2, 0x00, 0x00, 0x48, 0xc2, 0x00, 0x00, 0x40, 0x42, 0x00, 0x00, 0x8c, 0xc2, 0x00, 0x00, 0x24, 0x42, 0x00, 0x00, 0xb8, 0xc2, 0x00, 0x00, 0x60, 0x42, 0x00, 0x00, 0x10, 0x41, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x88, 0x42, 0x00, 0x00, 0x10, 0x42, 0x00, 0x00, 0x30, 0x42, 0x00, 0x00, 0xf0, 0xc1, 0x00, 0x00, 0x34, 0x42, 0x00, 0x00, 0x08, 0x42, 0x00, 0x00, 0x5c, 0x42, 0x00, 0x00, 0xc8, 0x41, 0x00, 0x00, 0x44, 0x42, 0x00, 0x00, 0x00, 0x41, 0x00, 0x00, 0x6c, 0x42, 0x00, 0x00, 0xd8, 0xc1, 0x00, 0x00, 0xae, 0x42, 0x00, 0x00, 0x8c, 0x42, 0x00, 0x00, 0xa2, 0x42, 0x00, 0x00, 0x88, 0x42, 0x00, 0x00, 0xa2, 0x42, 0x00, 0x00, 0x80, 0x40, 0x00, 0x00, 0x04, 0x42, 0x00, 0x00, 0x80, 0x3f, 0x00, 0x00, 0x2c, 0x42, 0x00, 0x00, 0x38, 0xc2, 0x00, 0x00, 0x88, 0xc2, 0x00, 0x00, 0x68, 0xc2, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0x9a, 0x42, 0x00, 0x00, 0x88, 0x41, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0xa0, 0xc2, 0x00, 0x00, 0x80, 0x3f, 0x00, 0x00, 0x90, 0x42, 0x00, 0x00, 0x80, 0xc0, 0x00, 0x00, 0x90, 0x42, 0x00, 0x00, 0x40, 0xc2, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xe0, 0xc1, 0x00, 0x00, 0x30, 0x41, 0x00, 0x00, 0x6c, 0x42, 0x00, 0x00, 0xa0, 0xc1, 0x00, 0x00, 0x0c, 0x42, 0x00, 0x00, 0x18, 0xc2, 0x00, 0x00, 0xb4, 0x42, 0x00, 0x00, 0x50, 0xc2, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0xd0, 0x41, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0xf0, 0xc1, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x30, 0xc1, 0x00, 0x00, 0x90, 0x41, 0x00, 0x00, 0x10, 0xc1, 0x00, 0x00, 0x2c, 0x42, 0x00, 0x00, 0xc0, 0xc1, 0x00, 0x00, 0x20, 0xc1, 0x00, 0x00, 0xb8, 0xc1, 0x00, 0x00, 0x20, 0xc1, 0x00, 0x00, 0x90, 0x42, 0x00, 0x00, 0x80, 0xc0, 0x00, 0x00, 0x68, 0x42, 0x00, 0x00, 0x20, 0x41, 0x00, 0x00, 0x82, 0xc2, 0x00, 0x00, 0x04, 0x42, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0x34, 0x42, 0x00, 0x00, 0x3c, 0xc2, 0x00, 0x00, 0x60, 0x42, 0x00, 0x00, 0x18, 0xc2, 0x00, 0x00, 0xe0, 0x40, 0x00, 0x00, 0x8a, 0x42, 0x00, 0x00, 0x9e, 0xc2, 0x00, 0x00, 0xba, 0x42, 0x00, 0x00, 0xa8, 0xc2, 0x00, 0x00, 0x86, 0x42, 0x00, 0x00, 0xbe, 0x42, 0x00, 0x00, 0x58, 0x42, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x98, 0xc2, 0x00, 0x00, 0x4c, 0x42, 0x00, 0x00, 0x9e, 0xc2, 0x00, 0x00, 0x18, 0x42, 0x00, 0x00, 0xba, 0x42, 0x00, 0x00, 0xb0, 0x41, 0x00, 0x00, 0xb6, 0x42, 0x00, 0x00, 0xc0, 0x40, 0x00, 0x00, 0xbc, 0xc2, 0x00, 0x00, 0x90, 0xc1, 0x00, 0x00, 0x96, 0xc2, 0x00, 0x00, 0x14, 0xc2, 0x00, 0x00, 0x14, 0x42, 0x00, 0x00, 0xe0, 0xc1, 0x00, 0x00, 0x50, 0x42, 0x00, 0x00, 0xb0, 0x41, 0x00, 0x00, 0x1c, 0x42, 0x00, 0x00, 0x34, 0x42, 0x00, 0x00, 0xa8, 0x41, 0x00, 0x00, 0x50, 0xc1, 0x00, 0x00, 0xa0, 0xc0, 0x00, 0x00, 0x54, 0x42, 0x00, 0x00, 0x80, 0x3f, 0x00, 0x00, 0x7c, 0x42, 0x00, 0x00, 0x30, 0xc1, 0x00, 0x00, 0xa0, 0x41, 0x00, 0x00, 0xd0, 0xc1, 0x00, 0x00, 0xc0, 0x41, 0x00, 0x00, 0xac, 0x42, 0x00, 0x00, 0xc4, 0xc2, 0x00, 0x00, 0x18, 0x42, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0xc0, 0xc1, 0x00, 0x00, 0xa0, 0x42, 0x00, 0x00, 0xc8, 0xc1, 0x00, 0x00, 0xa4, 0x42, 0x00, 0x00, 0x10, 0x41, 0x00, 0x00, 0x94, 0xc2, 0x00, 0x00, 0x04, 0xc2, 0x00, 0x00, 0xa4, 0xc2, 0x00, 0x00, 0x14, 0x42, 0x00, 0x00, 0xb2, 0xc2, 0x00, 0x00, 0x08, 0x42, 0x00, 0x00, 0x64, 0xc2, 0x00, 0x00, 0x64, 0x42, 0x00, 0x00, 0x70, 0x42, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x14, 0x42, 0x00, 0x00, 0xbe, 0xc2, 0x00, 0x00, 0x08, 0x42, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0xae, 0xc2, 0x00, 0x00, 0x88, 0xc1, 0x00, 0x00, 0xb2, 0xc2, 0x00, 0x00, 0x00, 0x40, 0x00, 0x00, 0xb8, 0x41, 0x00, 0x00, 0x80, 0x42, 0x00, 0x00, 0xd0, 0x41, 0x00, 0x00, 0x4c, 0x42, 0x00, 0x00, 0xb8, 0xc1, 0x00, 0x00, 0xc4, 0x42, 0x00, 0x00, 0x60, 0x42, 0x00, 0x00, 0xb2, 0x42, 0x00, 0x00, 0xc0, 0x41, 0x00, 0x00, 0xa0, 0x40, 0x00, 0x00, 0xa0, 0x41, 0x00, 0x00, 0x70, 0x41, 0x00, 0x00, 0x28, 0xc2, 0x00, 0x00, 0x64, 0x42, 0x00, 0x00, 0x14, 0xc2, 0x00, 0x00, 0x6c, 0x42, 0x00, 0x00, 0x9e, 0x42, 0x00, 0x00, 0x3c, 0xc2, 0x00, 0x00, 0x90, 0x42, 0x00, 0x00, 0x68, 0xc2, 0x00, 0x00, 0x80, 0x40, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x80, 0x40, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xbc, 0xc2, 0x00, 0x00, 0x30, 0xc2, 0x00, 0x00, 0xbe, 0xc2, 0x00, 0x00, 0x58, 0xc2, 0x00, 0x00, 0x98, 0x42, 0x00, 0x00, 0x30, 0xc1, 0x00, 0x00, 0x34, 0x42, 0x00, 0x00, 0x80, 0xc0, 0x00, 0x00, 0x50, 0xc1, 0x00, 0x00, 0x68, 0xc2, 0x00, 0x00, 0x70, 0xc1, 0x00, 0x00, 0x9a, 0xc2, 0x00, 0x00, 0xa2, 0x42, 0x00, 0x00, 0xbc, 0x42, 0x00, 0x00, 0xa0, 0x42, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x64, 0xc2, 0x00, 0x00, 0x80, 0xc2, 0x00, 0x00, 0x50, 0xc2, 0x00, 0x00, 0x92, 0xc2, 0x00, 0x00, 0x2c, 0xc2, 0x00, 0x00, 0x34, 0x42, 0x00, 0x00, 0x08, 0xc2, 0x00, 0x00, 0x34, 0x42, 0x00, 0x00, 0x60, 0x41, 0x00, 0x00, 0x98, 0xc1, 0x00, 0x00, 0xe0, 0x41, 0x00, 0x00, 0x96, 0xc2, 0x00, 0x00, 0x00, 0x41, 0x00, 0x00, 0x54, 0x42, 0x00, 0x00, 0xc0, 0x40, 0x00, 0x00, 0x60, 0x42, 0x00, 0x00, 0x5c, 0x42, 0x00, 0x00, 0x96, 0x42, 0x00, 0x00, 0x34, 0x42, 0x00, 0x00, 0x9a, 0x42, 0x00, 0x00, 0x78, 0x42, 0x00, 0x00, 0xa0, 0xc0, 0x00, 0x00, 0x38, 0x42, 0x00, 0x00, 0x00, 0xc0, 0x00, 0x00, 0x2c, 0x42, 0x00, 0x00, 0x08, 0x42, 0x00, 0x00, 0x68, 0x42, 0x00, 0x00, 0x70, 0x41, 0x00, 0x00, 0x70, 0xc1, 0x00, 0x00, 0x40, 0x40, 0x00, 0x00, 0x00, 0x40, 0x00, 0x00, 0x20, 0x41, 0x00, 0x00, 0xa8, 0xc2, 0x00, 0x00, 0x74, 0x42, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x94, 0xc2, 0x00, 0x00, 0xc0, 0x41, 0x00, 0x00, 0xa4, 0xc2, 0x00, 0x00, 0xf8, 0x41, 0x00, 0x00, 0x74, 0x42, 0x00, 0x00, 0xe0, 0x40, 0x00, 0x00, 0x92, 0x42, 0x00, 0x00, 0xa0, 0xc0, 0x00, 0x00, 0xe0, 0x40, 0x00, 0x00, 0xf0, 0x42, 0x00, 0x00, 0xc2, 0x42, 0x00, 0x00, 0x2c, 0x43, 0x00, 0x00, 0x0c, 0x42, 0x00, 0x00, 0x58, 0x42, 0x00, 0x00, 0x3c, 0x42, 0x00, 0x00, 0x94, 0x42, 0x00, 0x00, 0x9e, 0xc2, 0x00, 0x00, 0x80, 0xc0, 0x00, 0x00, 0xb0, 0xc2, 0x00, 0x00, 0xa0, 0xc0, 0x00, 0x00, 0x7c, 0xc2, 0x00, 0x00, 0xe0, 0xc1, 0x00, 0x00, 0x82, 0xc2, 0x00, 0x00, 0x10, 0x41, 0x00, 0x00, 0x54, 0x42, 0x00, 0x00, 0xe0, 0xc1, 0x00, 0x00, 0x7c, 0x42, 0x00, 0x00, 0xc4, 0xc2, 0x00, 0x00, 0xb8, 0x42, 0x00, 0x00, 0xaa, 0xc2, 0x00, 0x00, 0xb6, 0x42, 0x00, 0x00, 0xc2, 0xc2, 0x00, 0x00, 0x38, 0x42, 0x00, 0x00, 0x04, 0x42, 0x00, 0x00, 0x18, 0x42, 0x00, 0x00, 0x18, 0x42, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x30, 0x42, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x64, 0x42, 0x00, 0x00, 0x30, 0x41, 0x00, 0x00, 0x44, 0x42, 0x00, 0x00, 0xf8, 0x41, 0x00, 0x00, 0xa4, 0x42, 0x00, 0x00, 0x14, 0x42, 0x00, 0x00, 0x34, 0xc2, 0x00, 0x00, 0xa0, 0x41, 0x00, 0x00, 0x1c, 0xc2, 0x00, 0x00, 0xb0, 0xc1, 0x00, 0x00, 0x2c, 0xc2, 0x00, 0x00, 0x28, 0xc2, 0x00, 0x00, 0x68, 0xc2, 0x00, 0x00, 0x10, 0x41, 0x00, 0x00, 0xf0, 0xc1, 0x00, 0x00, 0x40, 0x41, 0x00, 0x00, 0xe0, 0xc1, 0x00, 0x00, 0xc8, 0x41, 0x00, 0x00, 0xa6, 0x42, 0x00, 0x00, 0xc8, 0x41, 0x00, 0x00, 0xae, 0x42, 0x00, 0x00, 0x8c, 0x42, 0x00, 0x00, 0xba, 0xc2, 0x00, 0x00, 0x82, 0x42, 0x00, 0x00, 0xb2, 0xc2, 0x00, 0x00, 0x90, 0xc1, 0x00, 0x00, 0xa8, 0xc2, 0x00, 0x00, 0xc8, 0x41, 0x00, 0x00, 0xa2, 0xc2, 0x00, 0x00, 0x80, 0x40, 0x00, 0x00, 0x92, 0xc2, 0x00, 0x00, 0xb8, 0x41, 0x00, 0x00, 0x92, 0xc2, 0x00, 0x00, 0x44, 0xc2, 0x00, 0x00, 0xae, 0x42, 0x00, 0x00, 0xb6, 0xc2, 0x00, 0x00, 0xaa, 0x42, 0x00, 0x00, 0x84, 0x42, 0x00, 0x00, 0x98, 0xc2, 0x00, 0x00, 0x78, 0x42, 0x00, 0x00, 0x92, 0xc2, 0x00, 0x00, 0x24, 0x42, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x18, 0x42, 0x00, 0x00, 0xd6, 0x42, 0x00, 0x00, 0x00, 0x42, 0x00, 0x00, 0xb0, 0xc1, 0x00, 0x00, 0x0c, 0x42, 0x00, 0x00, 0x90, 0xc1, 0x00, 0x00, 0x86, 0xc2, 0x00, 0x00, 0xa8, 0xc2, 0x00, 0x00, 0x90, 0xc2, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0xc0, 0x42, 0x00, 0x00, 0x20, 0x41, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x24, 0xc2, 0x00, 0x00, 0xd8, 0x41, 0x00, 0x00, 0x50, 0xc2, 0x00, 0x00, 0xb8, 0x41, 0x00, 0x00, 0x40, 0xc2, 0x00, 0x00, 0x8e, 0x42, 0x00, 0x00, 0xac, 0xc2, 0x00, 0x00, 0x80, 0x42, 0x00, 0x00, 0xa2, 0xc2, 0x00, 0x00, 0x70, 0xc2, 0x00, 0x00, 0xd0, 0xc1, 0x00, 0x00, 0x38, 0xc2, 0x00, 0x00, 0x90, 0xc1, 0x00, 0x00, 0x80, 0x42, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x82, 0x42, 0x00, 0x00, 0x80, 0x3f, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0x64, 0x42, 0x00, 0x00, 0xc6, 0xc2, 0x00, 0x00, 0x68, 0x42, 0x00, 0x00, 0xb0, 0xc2, 0x00, 0x00, 0xf0, 0x41, 0x00, 0x00, 0xaa, 0xc2, 0x00, 0x00, 0xf0, 0x41, 0x00, 0x00, 0x92, 0x42, 0x00, 0x00, 0x88, 0x42, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x86, 0x42, 0x00, 0x00, 0x70, 0x41, 0x00, 0x00, 0x88, 0x42, 0x00, 0x00, 0x90, 0x41, 0x00, 0x00, 0x8c, 0x42, 0x00, 0x00, 0xb6, 0x42, 0x00, 0x00, 0x9c, 0x42, 0x00, 0x00, 0xc2, 0x42, 0x00, 0x00, 0xa0, 0xc2, 0x00, 0x00, 0x10, 0xc1, 0x00, 0x00, 0xa2, 0xc2, 0x00, 0x00, 0xc0, 0xc0, 0x00, 0x00, 0xae, 0x42, 0x00, 0x00, 0x64, 0x42, 0x00, 0x00, 0x92, 0x42, 0x00, 0x00, 0x84, 0x42, 0x00, 0x00, 0x8a, 0x42, 0x00, 0x00, 0x24, 0x42, 0x00, 0x00, 0x98, 0x42, 0x00, 0x00, 0x24, 0x42, 0x00, 0x00, 0x00, 0xc2, 0x00, 0x00, 0x40, 0x41, 0x00, 0x00, 0xf8, 0xc1, 0x00, 0x00, 0x30, 0x41, 0x00, 0x00, 0x30, 0x42, 0x00, 0x00, 0x30, 0x42, 0x00, 0x00, 0x2c, 0x42, 0x00, 0x00, 0x4c, 0x42, 0x00, 0x00, 0xf8, 0xc1, 0x00, 0x00, 0x9c, 0x42, 0x00, 0x00, 0x18, 0xc2, 0x00, 0x00, 0x96, 0x42, 0x00, 0x00, 0x80, 0x42, 0x00, 0x00, 0x08, 0xc2, 0x00, 0x00, 0xae, 0x42, 0x00, 0x00, 0x04, 0xc2, 0x00, 0x00, 0xae, 0x42, 0x00, 0x00, 0x86, 0xc2, 0x00, 0x00, 0xa0, 0x42, 0x00, 0x00, 0xa0, 0xc2, 0x00, 0x00, 0x44, 0xc2, 0x00, 0x00, 0x98, 0x42, 0x00, 0x00, 0x20, 0xc2, 0x00, 0x00, 0x9c, 0x42, 0x00, 0x00, 0x1c, 0x42, 0x00, 0x00, 0x5c, 0xc2, 0x00, 0x00, 0x18, 0x42, 0x00, 0x00, 0x70, 0xc2, 0x00, 0x00, 0x50, 0xc1, 0x00, 0x00, 0x50, 0xc2, 0x00, 0x00, 0xb0, 0xc1, 0x00, 0x00, 0x34, 0xc2, 0x00, 0x00, 0xa6, 0xc2, 0x00, 0x00, 0xa8, 0x42, 0x00, 0x00, 0xaa, 0xc2, 0x00, 0x00, 0x96, 0x42, 0x00, 0x00, 0x82, 0xc2, 0x00, 0x00, 0x20, 0xc1, 0x00, 0x00, 0x8a, 0xc2, 0x00, 0x00, 0x10, 0x41, 0x00, 0x00, 0xe0, 0x40, 0x00, 0x00, 0x30, 0x42, 0x00, 0x00, 0x00, 0x40, 0x00, 0x00, 0x2c, 0x42, 0x00, 0x00, 0x9c, 0x42, 0x00, 0x00, 0x70, 0x42, 0x00, 0x00, 0x98, 0x42, 0x00, 0x00, 0x40, 0x42, 0x00, 0x00, 0x84, 0x42, 0x00, 0x00, 0x34, 0xc2, 0x00, 0x00, 0xaa, 0x42, 0x00, 0x00, 0x14, 0xc2, 0x00, 0x00, 0xc8, 0xc1, 0x00, 0x00, 0x70, 0xc2, 0x00, 0x00, 0x88, 0xc1, 0x00, 0x00, 0x86, 0xc2, 0x00, 0x00, 0xc8, 0x41, 0x00, 0x00, 0x4c, 0x42, 0x00, 0x00, 0xa0, 0x41, 0x00, 0x00, 0x3c, 0x42, 0x00, 0x00, 0x8a, 0xc2, 0x00, 0x00, 0x00, 0x42, 0x00, 0x00, 0xa4, 0xc2, 0x00, 0x00, 0x10, 0x41, 0x00, 0x00, 0xd8, 0xc1, 0x00, 0x00, 0x96, 0xc2, 0x00, 0x00, 0xc0, 0xc1, 0x00, 0x00, 0x82, 0xc2, 0x00, 0x00, 0x24, 0x42, 0x00, 0x00, 0x80, 0x42, 0x00, 0x00, 0x50, 0x42, 0x00, 0x00, 0x74, 0x42, 0x00, 0x00, 0x88, 0xc2, 0x00, 0x00, 0x1c, 0xc2, 0x00, 0x00, 0x5c, 0xc2, 0x00, 0x00, 0x58, 0xc2, 0x00, 0x00, 0x70, 0xc1, 0x00, 0x00, 0x6c, 0xc2, 0x00, 0x00, 0xf0, 0xc1, 0x00, 0x00, 0x58, 0xc2, 0x00, 0x00, 0x74, 0xc2, 0x00, 0x00, 0x5c, 0xc2, 0x00, 0x00, 0x70, 0xc2, 0x00, 0x00, 0x50, 0xc2, 0x00, 0x00, 0xc8, 0x41, 0x00, 0x00, 0xb0, 0xc2, 0x00, 0x00, 0xb8, 0x41, 0x00, 0x00, 0xa6, 0xc2, 0x00, 0x00, 0x82, 0x42, 0x00, 0x00, 0x14, 0x42, 0x00, 0x00, 0x48, 0x42, 0x00, 0x00, 0xd0, 0x41, 0x00, 0x00, 0xa0, 0xc1, 0x00, 0x00, 0xb2, 0x42, 0x00, 0x00, 0xc8, 0xc1, 0x00, 0x00, 0xac, 0x42, 0x00, 0x00, 0x50, 0xc2, 0x00, 0x00, 0xa2, 0xc2, 0x00, 0x00, 0x70, 0xc2, 0x00, 0x00, 0x84, 0xc2, 0x00, 0x00, 0x86, 0x42, 0x00, 0x00, 0x90, 0x42, 0x00, 0x00, 0x70, 0x42, 0x00, 0x00, 0xa2, 0x42, 0x00, 0x00, 0x9e, 0xc2, 0x00, 0x00, 0xb8, 0x41, 0x00, 0x00, 0x0b, 0xc3, 0x00, 0x00, 0xd8, 0xc1, 0x00, 0x00, 0xac, 0xc2, 0x00, 0x00, 0x00, 0xc0, 0x00, 0x00, 0xae, 0xc2, 0x00, 0x00, 0x80, 0xbf, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0x10, 0x42, 0x00, 0x00, 0x38, 0xc2, 0x00, 0x00, 0xf0, 0x41, 0x00, 0x00, 0xb8, 0xc2, 0x00, 0x00, 0x68, 0x42, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0xba, 0x42, 0x00, 0x00, 0x80, 0x3f, 0x00, 0x00, 0xb2, 0xc2, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xa8, 0xc2, 0x00, 0x00, 0xa6, 0xc2, 0x00, 0x00, 0x80, 0xc1, 0x00, 0x00, 0x84, 0xc2, 0x00, 0x00, 0x4c, 0xc2, 0x00, 0x00, 0x40, 0xc1, 0x00, 0x00, 0x50, 0x42, 0x00, 0x00, 0x10, 0xc1, 0x00, 0x00, 0x58, 0x42, 0x00, 0x00, 0x28, 0x42, 0x00, 0x00, 0xa2, 0x42, 0x00, 0x00, 0x0c, 0x42, 0x00, 0x00, 0x84, 0x42, 0x00, 0x00, 0xb4, 0x42, 0x00, 0x00, 0xa6, 0x42, 0x00, 0x00, 0xb0, 0x42, 0x00, 0x00, 0xa8, 0x42, 0x00, 0x00, 0xae, 0x42, 0x00, 0x00, 0x40, 0x42, 0x00, 0x00, 0xc4, 0x42, 0x00, 0x00, 0x4c, 0x42, 0x00, 0x00, 0x20, 0xc2, 0x00, 0x00, 0x80, 0xc1, 0x00, 0x00, 0x14, 0xc2, 0x00, 0x00, 0x80, 0x40, 0x00, 0x00, 0x5c, 0xc2, 0x00, 0x00, 0x9c, 0xc2, 0x00, 0x00, 0x96, 0xc2, 0x00, 0x00, 0x94, 0xc2, 0x00, 0x00, 0x82, 0x42, 0x00, 0x00, 0xb8, 0x41, 0x00, 0x00, 0x64, 0x42, 0x00, 0x00, 0xf0, 0x41, 0x00, 0x00, 0xb8, 0x41, 0x00, 0x00, 0x88, 0x41, 0x00, 0x00, 0x90, 0x41, 0x00, 0x00, 0x28, 0x42, 0x00, 0x00, 0x08, 0x42, 0x00, 0x00, 0x92, 0x42, 0x00, 0x00, 0xe0, 0x41, 0x00, 0x00, 0x96, 0x42, 0x00, 0x00, 0x60, 0x41, 0x00, 0x00, 0xc2, 0x42, 0x00, 0x00, 0x70, 0x41, 0x00, 0x00, 0xc4, 0x42, 0x00, 0x00, 0x0c, 0x42, 0x00, 0x00, 0x2c, 0xc2, 0x00, 0x00, 0x14, 0x42, 0x00, 0x00, 0x30, 0xc2, 0x00, 0x00, 0x18, 0xc2, 0x00, 0x00, 0x50, 0x41, 0x00, 0x00, 0xe0, 0xc1, 0x00, 0x00, 0x50, 0x41, 0x00, 0x00, 0x50, 0x41, 0x00, 0x00, 0x68, 0x42, 0x00, 0x00, 0x30, 0x41, 0x00, 0x00, 0x68, 0x42, 0x00, 0x00, 0x50, 0xc2, 0x00, 0x00, 0xe0, 0xc1, 0x00, 0x00, 0x18, 0xc2, 0x00, 0x00, 0x58, 0xc2, 0x00, 0x00, 0xc0, 0x41, 0x00, 0x00, 0xd8, 0xc1, 0x00, 0x00, 0x80, 0xbf, 0x00, 0x00, 0x18, 0x42, 0x00, 0x00, 0x28, 0x42, 0x00, 0x00, 0x7c, 0x42, 0x00, 0x00, 0x34, 0x42, 0x00, 0x00, 0x54, 0x42, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x60, 0xc1, 0x00, 0x00, 0xa0, 0x40, 0x00, 0x00, 0xa8, 0xc1, 0x00, 0x00, 0x20, 0x42, 0x00, 0x00, 0x68, 0x42, 0x00, 0x00, 0x24, 0x42, 0x00, 0x00, 0x6c, 0x42, 0x00, 0x00, 0xa0, 0x40, 0x00, 0x00, 0x20, 0x41, 0x00, 0x00, 0xe0, 0x40, 0x00, 0x00, 0x30, 0x41, 0x00, 0x00, 0x90, 0x41, 0x00, 0x00, 0x48, 0x42, 0x00, 0x00, 0x50, 0x41, 0x00, 0x00, 0x48, 0x42, 0x00, 0x00, 0x60, 0x42, 0x00, 0x00, 0x8c, 0x42, 0x00, 0x00, 0x68, 0x42, 0x00, 0x00, 0x9c, 0x42, 0x00, 0x00, 0x0c, 0xc2, 0x00, 0x00, 0x3c, 0xc2, 0x00, 0x00, 0x20, 0xc2, 0x00, 0x00, 0x38, 0xc2, 0x00, 0x00, 0xc2, 0xc2, 0x00, 0x00, 0x96, 0xc2, 0x00, 0x00, 0x8c, 0xc2, 0x00, 0x00, 0xb0, 0xc2, 0x00, 0x00, 0x9a, 0x42, 0x00, 0x00, 0x34, 0x42, 0x00, 0x00, 0x6c, 0x42, 0x00, 0x00, 0x74, 0x42, 0x00, 0x00, 0xc0, 0xc0, 0x00, 0x00, 0x94, 0xc2, 0x00, 0x00, 0xa0, 0x40, 0x00, 0x00, 0x86, 0xc2, 0x00, 0x00, 0xa0, 0xc2, 0x00, 0x00, 0x2c, 0xc2, 0x00, 0x00, 0x96, 0xc2, 0x00, 0x00, 0x5c, 0xc2, 0x00, 0x00, 0x08, 0x42, 0x00, 0x00, 0x00, 0xc1, 0x00, 0x00, 0xc0, 0x41, 0x00, 0x00, 0xd0, 0xc1, 0x00, 0x00, 0xae, 0x42, 0x00, 0x00, 0xa0, 0xc2, 0x00, 0x00, 0xba, 0x42, 0x00, 0x00, 0x8e, 0xc2, 0x00, 0x00, 0x88, 0xc2, 0x00, 0x00, 0x84, 0x42, 0x00, 0x00, 0x70, 0xc2, 0x00, 0x00, 0xa4, 0x42, 0x00, 0x00, 0x8e, 0x42, 0x00, 0x00, 0x4c, 0x42, 0x00, 0x00, 0x74, 0x42, 0x00, 0x00, 0x78, 0x42, 0x00, 0x00, 0x38, 0x42, 0x00, 0x00, 0x04, 0xc2, 0x00, 0x00, 0x50, 0x42, 0x00, 0x00, 0x04, 0xc2, 0x00, 0x00, 0x00, 0x42, 0x00, 0x00, 0x18, 0x42, 0x00, 0x00, 0x08, 0x42, 0x00, 0x00, 0x20, 0x42, 0x00, 0x00, 0x88, 0x42, 0x00, 0x00, 0xa0, 0xc0, 0x00, 0x00, 0x9e, 0x42, 0x00, 0x00, 0x20, 0xc1, 0x00, 0x00, 0x3c, 0xc2, 0x00, 0x00, 0xb6, 0xc2, 0x00, 0x00, 0x44, 0xc2, 0x00, 0x00, 0xc2, 0xc2, 0x00, 0x00, 0x54, 0xc2, 0x00, 0x00, 0x10, 0x41, 0x00, 0x00, 0x24, 0xc2, 0x00, 0x00, 0x60, 0x41, 0x00, 0x00, 0xba, 0x42, 0x00, 0x00, 0x96, 0xc2, 0x00, 0x00, 0xb8, 0x42, 0x00, 0x00, 0x96, 0xc2, 0x00, 0x00, 0x86, 0xc2, 0x00, 0x00, 0xc0, 0xc2, 0x00, 0x00, 0x70, 0xc2, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0xa8, 0x41, 0x00, 0x00, 0xf0, 0xc1, 0x00, 0x00, 0xb8, 0x41, 0x00, 0x00, 0x00, 0xc2, 0x00, 0x00, 0xe0, 0x40, 0x00, 0x00, 0x3c, 0x42, 0x00, 0x00, 0x30, 0x41, 0x00, 0x00, 0x5c, 0x42, 0x00, 0x00, 0x00, 0xc0, 0x00, 0x00, 0xb4, 0x42, 0x00, 0x00, 0xd8, 0x41, 0x00, 0x00, 0xa0, 0x42, 0x00, 0x00, 0x86, 0x42, 0x00, 0x00, 0x82, 0xc2, 0x00, 0x00, 0x7c, 0x42, 0x00, 0x00, 0x6c, 0xc2, 0x00, 0x00, 0x10, 0xc2, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x1c, 0xc2, 0x00, 0x00, 0xd0, 0x42, 0x00, 0x00, 0xa8, 0x41, 0x00, 0x00, 0x96, 0xc2, 0x00, 0x00, 0xb0, 0x41, 0x00, 0x00, 0x92, 0xc2, 0x00, 0x00, 0x8a, 0xc2, 0x00, 0x00, 0x00, 0x40, 0x00, 0x00, 0x88, 0xc2, 0x00, 0x00, 0x40, 0x40, 0x00, 0x00, 0xb0, 0x41, 0x00, 0x00, 0xf8, 0x41, 0x00, 0x00, 0xc0, 0x41, 0x00, 0x00, 0x28, 0x42, 0x00, 0x00, 0xb2, 0xc2, 0x00, 0x00, 0x84, 0x42, 0x00, 0x00, 0xba, 0xc2, 0x00, 0x00, 0x80, 0x42, 0x00, 0x00, 0xb4, 0x42, 0x00, 0x00, 0x4c, 0x42, 0x00, 0x00, 0xb6, 0x42, 0x00, 0x00, 0x4c, 0x42, 0x00, 0x00, 0xb6, 0x42, 0x00, 0x00, 0xa8, 0xc2, 0x00, 0x00, 0x9e, 0x42, 0x00, 0x00, 0xb4, 0xc2, 0x00, 0x00, 0x24, 0xc2, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x24, 0xc2, 0x00, 0x00, 0xbe, 0x42, 0x00, 0x00, 0xb8, 0xc1, 0x00, 0x00, 0x74, 0xc2, 0x00, 0x00, 0xb0, 0xc1, 0x00, 0x00, 0x6c, 0xc2, 0x00, 0x00, 0x18, 0x42, 0x00, 0x00, 0x38, 0x42, 0x00, 0x00, 0x00, 0x42, 0x00, 0x00, 0x50, 0x42, 0x00, 0x00, 0x1c, 0xc2, 0x00, 0x00, 0xc0, 0xc1, 0x00, 0x00, 0x24, 0xc2, 0x00, 0x00, 0x80, 0xc0, 0x00, 0x00, 0xd8, 0xc1, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0x70, 0xc1, 0x00, 0x00, 0xb0, 0xc2, 0x00, 0x00, 0xb0, 0x42, 0x00, 0x00, 0xc8, 0x42, 0x00, 0x00, 0x9a, 0x42, 0x00, 0x00, 0xd0, 0x42, 0x00, 0x00, 0x68, 0x42, 0x00, 0x00, 0x10, 0x42, 0x00, 0x00, 0x68, 0x42, 0x00, 0x00, 0x04, 0x42, 0x00, 0x00, 0xc0, 0xc1, 0x00, 0x00, 0xd0, 0xc1, 0x00, 0x00, 0xb0, 0xc1, 0x00, 0x00, 0x00, 0xc2, 0x00, 0x00, 0x4c, 0xc2, 0x00, 0x00, 0x00, 0x42, 0x00, 0x00, 0xc6, 0xc2, 0x00, 0x00, 0x64, 0x42, 0x00, 0x00, 0xc8, 0xc2, 0x00, 0x00, 0xb8, 0x41, 0x00, 0x00, 0xb2, 0xc2, 0x00, 0x00, 0xc0, 0x41, 0x00, 0x00, 0x48, 0x42, 0x00, 0x00, 0x50, 0xc1, 0x00, 0x00, 0x60, 0x42, 0x00, 0x00, 0x30, 0xc1, 0x00, 0x00, 0x4c, 0xc2, 0x00, 0x00, 0xb2, 0xc2, 0x00, 0x00, 0x54, 0xc2, 0x00, 0x00, 0xb2, 0xc2 ]
function bytes_to_float(data) {
var buf = new Uint8Array(data).buffer
// Create a data view of it
var view = new DataView(buf);
return view.getFloat32(0);
}
let x = 100
let y = 90
let done = 0;
function setup() {
createCanvas(600, 600);
background(220);
strokeWeight(1);
for (let i = 0; i < 195; ++i) {
let b = i * 16;
x1 = bytes_to_float(li.slice(b + 0, b + 4).toReversed()) * 2;
y1 = bytes_to_float(li.slice(b + 4, b + 8).toReversed()) * 2;
x2 = bytes_to_float(li.slice(b + 8, b + 12).toReversed()) * 2;
y2 = bytes_to_float(li.slice(b + 12, b + 16).toReversed()) * 2;
line(x1 + 300, y1 + 300, x2 + 300, y2 + 300);
}
strokeWeight(7);
stroke('red');
point(300, 300);
stroke('purple');
point(300 + x * 2, 300 + y * 2);
strokeWeight(1);
stroke('green');
}
let points = [[x, y]]
let sol = "";
function toAngle(nx, ny) {
dx = nx - x;
dy = ny - y;
angle = atan2(dy, dx);
if (angle < 0)
angle += 2 * PI
let k = angle / PI / 2
if (k < 0 || k > 1) {
console.log("NOT OK!!!")
}
k = round(k * 675)
let b_1 = String.fromCharCode((k % 26) + 65)
k = (k - (k % 26)) / 26;
let b_0 = String.fromCharCode(k + 65)
return `${b_0}${b_1}`;
}
function fromAngle(s) {
k = ((s.charCodeAt(0) - 65) * 26 + s.charCodeAt(1) - 65) / 675;
k *= 2 * PI;
return k;
}
function toMag(nx, ny) {
d = dist(nx, ny, x, y);
if (d > 25) d = 25;
d = round(d * 675 / 25)
b_3 = String.fromCharCode((d % 26) + 65)
d /= 26
b_2 = String.fromCharCode(d + 65)
return `${b_2}${b_3}`;
}
function fromMag(s) {
k = (s.charCodeAt(0) - 65) * 26 + s.charCodeAt(1) - 65;
k = k / 675.0 * 25.0;
return k;
}
function orientation(ax, ay, bx, by, cx, cy) {
if ((bx - ax) * (cy - ay) <= (cx - ax) * (by - ay)) {
return 0;
}
return 1;
}
function intersect(nx, ny, l1x, l1y, l2x, l2y) {
o1 = orientation(x, y, l1x, l1y, l2x, l2y)
o2 = orientation(nx, ny, l1x, l1y, l2x, l2y);
o3 = orientation(x, y, nx, ny, l1x, l1y);
o4 = orientation(x, y, nx, ny, l2x, l2y);
if (o1 != o2 && o3 != o4) {
return 1;
}
// console.log(o1, o2, o3, o4)
return 0;
}
function check(nx, ny) {
print(x, y, nx, ny)
for (let i = 0; i < 195; ++i) {
let b = i * 16;
x1 = bytes_to_float(li.slice(b + 0, b + 4).toReversed());
y1 = bytes_to_float(li.slice(b + 4, b + 8).toReversed());
x2 = bytes_to_float(li.slice(b + 8, b + 12).toReversed());
y2 = bytes_to_float(li.slice(b + 12, b + 16).toReversed());
if (intersect(nx, ny, x1, y1, x2, y2)) {
strokeWeight(3);
stroke('red');
line(x1 * 2 + 300, y1 * 2 + 300, x2 * 2 + 300, y2 * 2 + 300);
return 0;
}
}
return 1;
}
function mouseClicked() {
new_x = (mouseX - 300) / 2;
new_y = (mouseY - 300) / 2;
// console.log(new_x, new_y);
A = toAngle(new_x, new_y);
angle = fromAngle(A);
D = toMag(new_x, new_y);
d = fromMag(D);
// console.log(angle, d);
new_x = x + cos(angle) * d;
new_y = y + sin(angle) * d;
if (!check(new_x, new_y)) {
console.log("NO");
return;
}
if (!done && dist(x, y, new_x, new_y) < 25) {
strokeWeight(1);
stroke('green');
line(x * 2 + 300, y * 2 + 300, new_x * 2 + 300, new_y *2 + 300);
strokeWeight(3);
stroke('purple');
x = new_x;
y = new_y;
point(x * 2 + 300, y * 2 + 300);
points.push([x , y]);
sol = sol + A + D;
console.log(x, y);
if (round(x) == 0 && round(y) == 0) {
// points.forEach((p) => {
// console.log(p[0], p[1]);
// });
console.log(sol);
done = 1;
}
}
}
let lastX = 0;
let lastY = 0;
function draw() {
// let newX = floor((mouseX - 300) / 2);
// let newY = floor((mouseY - 300) / 2);
// console.log(newX, newY, dist(x, y, newX, newY));
// if (newX != lastX || newY != lastY) {
// strokeWeight(5);
// stroke(220);
// point((lastX + 300) * 2, (lastY + 300) * 2);
// stroke('blue');
// point((newX + 300) * 2, (newY + 300) * 2);
// lastX = newX;
// lastY = newY;
// }
}
References
binary analysis platform base on concolic execution: https://angr.io/ ↩︎
JavaScript library for creative coding: https://p5js.org/ ↩︎